PID控制算法与在模拟电路中应用研究

**摘要：**PID控制算法作为一种广泛应用于工程实践系统中的经典控制算法，凭借其简便、可靠的特点在简单运动控制中发挥着至关重要的作用。以一个学生的角度，从简略的介绍PID的历史发展引入，重点综述PID控制器的算法设计，同时引入目前在运动控制中被广泛应用的位置式PID算法，增量式PID算法，最后结合目前所学模拟电子知识进行简要设计仿真，并进一步对未来PID控制算法发展进行粗略展望。

**关键词：**PID控制算法；运动控制；位置式；增量式；

Abstract: PID control algorithm, as a classic control algorithm, which was widely used in engineering practice systems, plays a significant role in simple motion control by its virtue of simplicity and reliability. From the perspective of a student, this paper starts by briefly introducing the PID historical development, focusing on the algorithm design of the PID controller, and introducing the positional PID algorithm and incremental PID algorithm that are widely used in motion control. Finally, combined with current analog electronics knowledge to carry out a brief design simulation, and make a rough outlook on the future development of PID control algorithms.

Keywords: PID control algorithm; Motion control; Positional; Incremental;

前言

PID控制算法是建立在反馈放大电路上的一种自动控制算法，其经过近百年的发展历史，在理论研究和技术应用层面已颇为成熟，基于PID调节器衍生出的改进型，如：专家系统PID控制器、自适应PID控制器以及模糊PID控制器等智能控制器，在牺牲一部分PID控制器简便、易用的特点的同时，提高了运动控制效果，增强了系统面对干扰的稳定性，取得了较好的试验成果[^1]。到本世纪初，PID控制器及其改进型仍是各种运动控制过程中最常见的控制器[^2]（世界范围超九成以上在过程控制中应用纯PID控制器及其改进型，后者占比较小，仅为6%左右）。但在基础运动控制过程中，输入曲线往往不具有线性时不变特征，难以用数学模型进行量化，只能手动调整参数，面临着参数调整困难、输出曲线超调和震荡等问题。针对PID控制器所面临的问题与挑战，国内外已有许多专家学者就此讨论了现状[^3]。这就对PID控制器的进一步深入研究提出了要求，本文通过对几种PID控制算法的简易介绍，指出其各自特色和适用环境，设计反向比例PID控制电路并进行仿真分析，以加深对PID系统设计的认识和了解，最后对PID的发展做出展望总结。

PID控制算法基本原理

基本PID控制原理

PID算法是集比例（Proportional）、积分（Integral）、微分（Differential）三部分为一体的二阶线性控制算法，其原始公式为：

u(t)=Kp[e(t)+TTi∫0te(t)dt+TdT∙de(t)dt](1)u\left(t\right)=K_p\left[e\left(t\right)+\frac{T}{T_i}\int_{0}^{t}e\left(t\right)dt+\frac{T_d}{T}\bullet\frac{de(t)}{dt}\right]\tag{1}

在(1)式中，为时刻PID控制系统的输入量，通常使用系统设定量与被控量采样值的差值，；为该系统的输出量; 是该系统的比例项的调节系数，积分系数为，微分系数为，其中、分别为系统的积分时间与微分时间，为系统对被控量的采样周期，具体如图 1系统控制原理图所示[^4]。

图 1 PID控制原理图

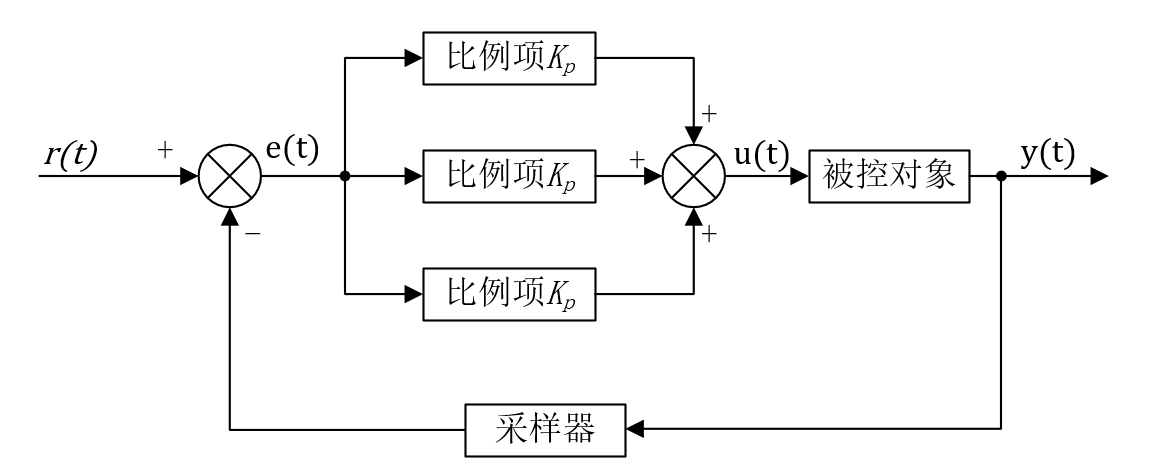
由于单片机或计算机等系统平台均为离散控制系统，不能对被控量进行时时采样处理，因此对(1)式简化后，离散化PID公式如下：

u(k)=Kpe(k)+Ki∑i=0ke(i)+Kd[e(k)−e(k−1)](2)u\left(k\right)=K_pe\left(k\right)+K_i\sum_{i=0}^{k}e\left(i\right)+K_d\left[e\left(k\right)-e(k-1)\right] \tag{2}

为PID控制系统第次运行的输入量，即系统第次采样值与设定值的偏差量，；为该系统的第次运行所对应的输出量。

位置式PID算法

位置式PID算法的表达式与(2)相同，系统的输出量与输入量呈一一对应的关系，系统根据第次的采样值与设定值的偏差实时计算出第次的输出量，从而直接控制运动系统，不断循环这个过程，使被控量能够稳定在系统设定值。

由于使用累加计算来代替积分项的积分计算，因此位置式PID控制算法更加适合不具有积分器件的系统，但同时也导致位置式PID算法在应用时存在计算量大的问题。

增量式PID算法

增量式PID作为位置式PID控制算法的改进型，将输出量的增量作为输出量。与位置式PID算法所不同，每个时刻的输出是相对当前输出量的增量，并非直接对应输出量的大小，所以被控系统在使用增量式PID算法时需要先对输出增量进行累加，然后实现对目标的控制。

下面给出的推导过程：

Δu(k)=u(k)−u(k−1)={Kpe(k)+Ki∑i=0ke(i)+Kd[e(k)−e(k−1)]}−{Kpe(k−1)+Ki∑i=0k−1e(i)+Kd[e(k−1)−e(k−2)]}=Kp[e(k)−e(k−1)]+Kie(k)+Kd[e(k)−2e(k−1)+e(k−2)]\begin{align*} \Delta u\left(k\right) & = u\left(k\right)-u\left(k-1\right)\\ & =\left\{K_pe\left(k\right)+K_i\sum_{i=0}^{k}e\left(i\right)+K_d\left[e\left(k\right)-e\left(k-1\right)\right]\right\}\\ & -\left\{K_pe\left(k-1\right)+K_i\sum_{i=0}^{k-1}e\left(i\right)+K_d\left[e\left(k-1\right)-e\left(k-2\right)\right]\right\}\\ & = K_p\left[e\left(k\right)-e\left(k-1\right)\right]+K_ie\left(k\right)+K_d\left[e\left(k\right)-2e\left(k-1\right)+e\left(k-2\right)\right]\tag{3}\\ \end{align*}

式中、和分别为PID三个部分的控制参数，为PID控制系统第次的输入量，前文已经有详细的介绍，便不再过多赘述。

两种PID算法的比较

位置式PID算法的优缺点分析

由上述原理可知，位置式PID算法的输出量可以直接对被控对象进行控制，系统的输出量与输入量一一对应，比例部分只与当前偏差有关，积分部分则是与之前系统偏差的累加和有关，微分部分则与当前偏差与上次偏差的差有关，相较增量式算法结构简单、清晰，对于参数的调整确定也较为明了。

但其缺点在上方也已提及，因为积分波分与之前每个时刻的偏差累计和有关，过去的每个状态都决定着当前系统的输出，使得系统的计算量不断增加，增大了系统平台的负担，减弱了系统的鲁棒性。另一个缺点在于积分饱和，当系统的设定值改变后，若小于被控对象采样值，偏差反向，但由于之前过大的积分积累值，输出量和被控量需要相当长的一段时间才能脱离饱和区，因此会引起控制系统产生大幅度超调，对系统的鲁棒性有较大影响。

因此在系统输入值的绝对值过大时，需要紧急停止积分项，当采样值接近设定值时，即小于某一阈值时，再开启积分项逐渐缩小系统静态误差，具体实现原理如下：

积分部分：ui(k)=Ki∑i=0ke(i)\text{积分部分：}u_i\left(k\right)=K_i\sum_{i=0}^{k}e\left(i\right)

e(k)={r(k)−y(k),∣r(k)−y(k)∣<emax0,else e(k) = \begin{cases} r\left(k\right)-y\left(k\right), & |r\left(k\right)-y\left(k\right)|<e_{max} \\ 0, & \text{else} \\ \end{cases}

因此位置式PID算法更加适合设定值为固定值，需要将被控对象被控量稳定在设定值附近的运动控制，如应用在平衡车的平衡控制，电单车的平衡控制等平衡控制中。同时在没有积分器件的运动控制系统中也能够得到较好的应用。

增量式PID算法的优缺点分析

正是由于位置式PID算法存在这些缺点，增量式PID算法才得以提出，它在前者的设计上加以改进。不再需要累加求和，减少了对系统平台的负担，控制增量仅与最近三次的输入偏差有关。另外系统将输出增量作为输出，即被控对象的输入变化量，当出现不正常变化时，可以通过逻辑判断来排除错误信息，增强了系统的鲁棒性。

但正是由于仅与最近三次的输入偏差有关，由于积分截断效应，可能会产生一定量的静态偏差。

因此增量式PID算法更适合设定值需要不断变化的运动控制中，如步进电机的控制和平衡车的速度环，在对此类的控制中有很好的实时性。[^5]

PID算法控制系统仿真

在上文中已经详细介绍了PID控制原理和两个在运动控制中被广泛应用的PID算法，并且独立分析了两者的优缺点，给出了各自适合的运动控制环境。下面将逐步利用Multisim搭建反向比例运算PID控制电路的积分部分和微分部分并进行仿真分析，最后将其组合以实现反向比例PID电路。

积分运算电路

积分运算电路的搭建和理论计算

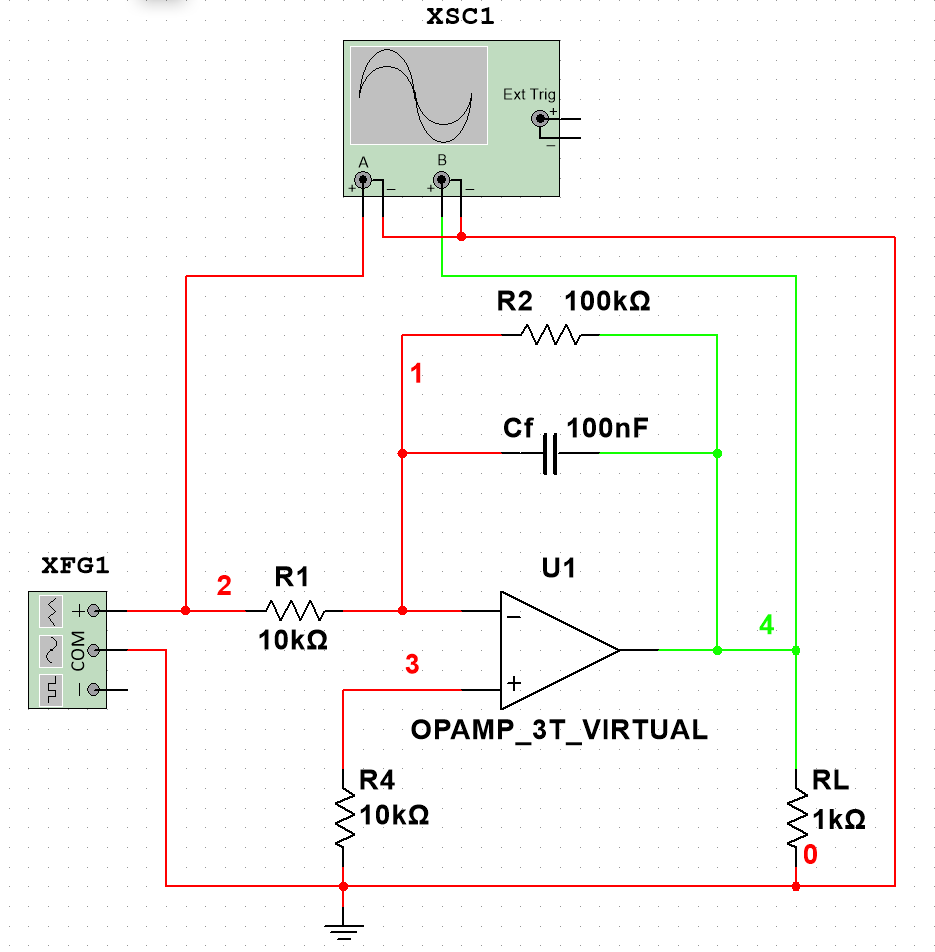
首先搭建积分运算电路，如右图 2。XFG1为交流信号源；XSC1为二通道示波器，在仿真利用A、B两通道来采集输入、输出信号，A通道采集信号源（信号源均采用1KHz信号），B通道采集电路系统的输出电压信号。

与一般的积分放大电路所不同，R2的在电路中发挥着抑制直流增益过大的作用。由反向比例运算放大电路的放大倍数的计算公式可知：

对于直流信号，若没有反馈电阻R2，反馈阻抗，放大倍数，会造成直流增益饱和。

而对于交流信号，只需使反馈电阻的阻抗远大于反馈电容容抗即可近似忽略R2所带来的影响。

、分别为交流信号源频率和反馈电容值，即1KHz和100nF，经计算，故在交流信号作用时，可近似忽略R2所带来的影响，因此便可利用电路知识计算得出输出电压表达式：

积分运算电路的仿真

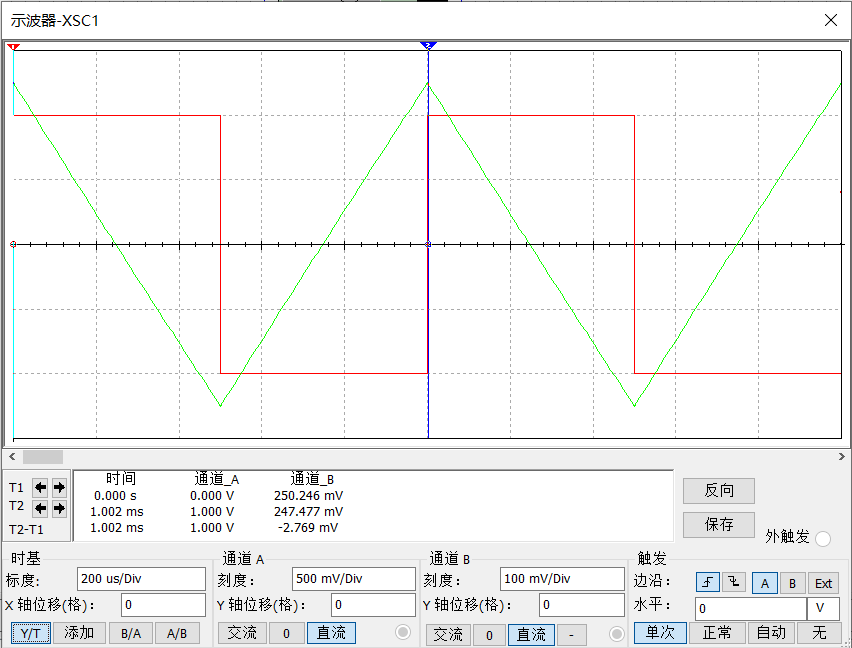
调节信号源使其先后输入频率，赋值的方波信号和正弦波信号，示波器采集波形分别如图 3和图 4。红色线为信号源波形，绿色线为输出信号波形，前后两次输入分别对应的输出波形为三角波和余弦波，符合数学计算。

经分析，交流放大倍数，如图 4中可见输出余弦波的赋值，与理论计算完全符合，存在的微小误差为反馈电阻R2所引起的，同时也印证了前文可近似忽略R2影响的判断。

图 3 输入方波信号
图 4 输入正弦波信号

微分运算电路

微分运算电路的搭建和理论计算

图 5 微分运算电路
与积分电路相似，关于电路搭建并不再赘述。

C1在此电路中发挥抑制交流增益过大的作用。对于直流信号，该电路不能正常工作；对于交流信号，若没有反馈电容C1，前置电容趋近于0，故交流放大倍数，会造成交流增益饱和。

因此，在应用时只需使反馈电容的容抗远大于反馈电阻阻抗，便可近似忽略C1所带来的影响。

经计算，，故在交流信号作用时，可近似忽略C1所带来的影响。因此便可利用电路知识计算得出输出电压表达式：

微分运算电路的仿真

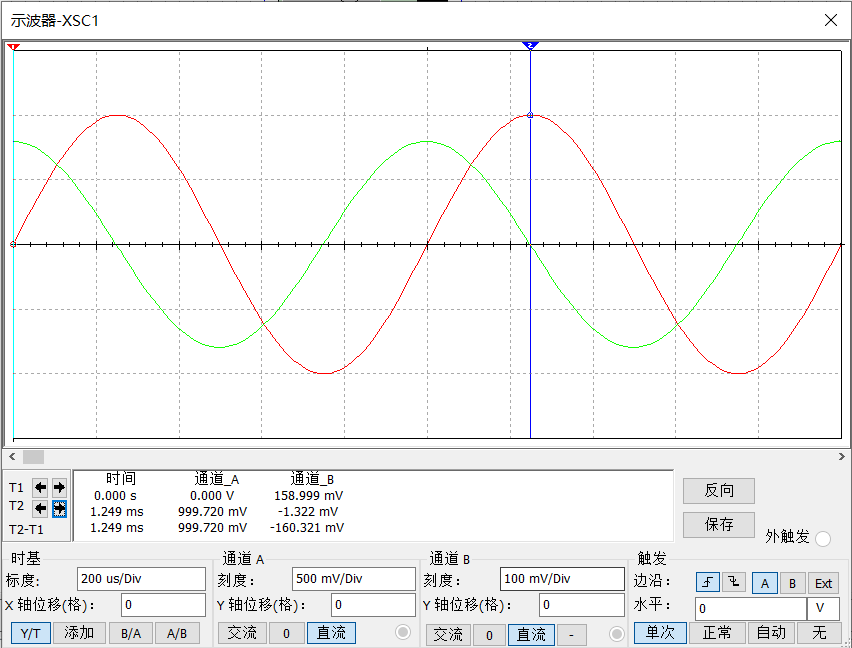
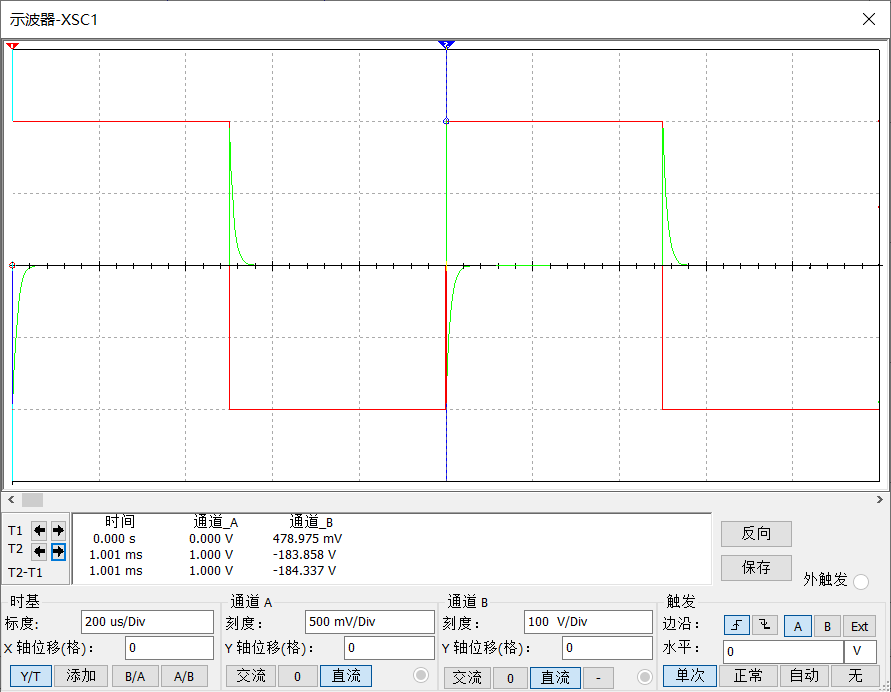
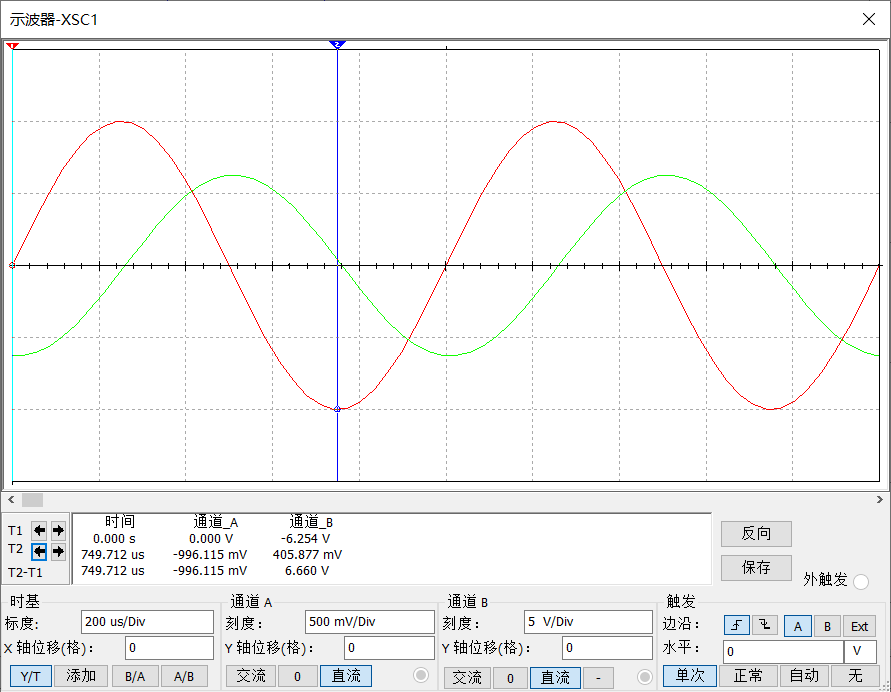
调节信号源使其先后输入频率，赋值的方波信号和正弦波信号，示波器采集波形分别如图 6和图 7。红色线为信号源波形，绿色线为输出信号波形，前后两次输入分别对应的输出波形分别为冲击波和反向余弦波，符合数学计算。

经分析，，交流放大倍数，如图 7中可见输出余弦波的赋值，与理论计算完全符合，存在的误差为反馈电容C1所引起的，同时也印证了前文可近似忽略C1影响的判断。

图 6 输入方波信号
图 7 输入正弦波信号

反向比例PID运算器电路

PID运算器电路的搭建和理论计算

图 8 PID电路
关于积分运算电路（积分部分）、微分运算电路（微分部分）已在前文做了详细介绍和电路仿真，所搭建的PID运算电路如右图 8所示。

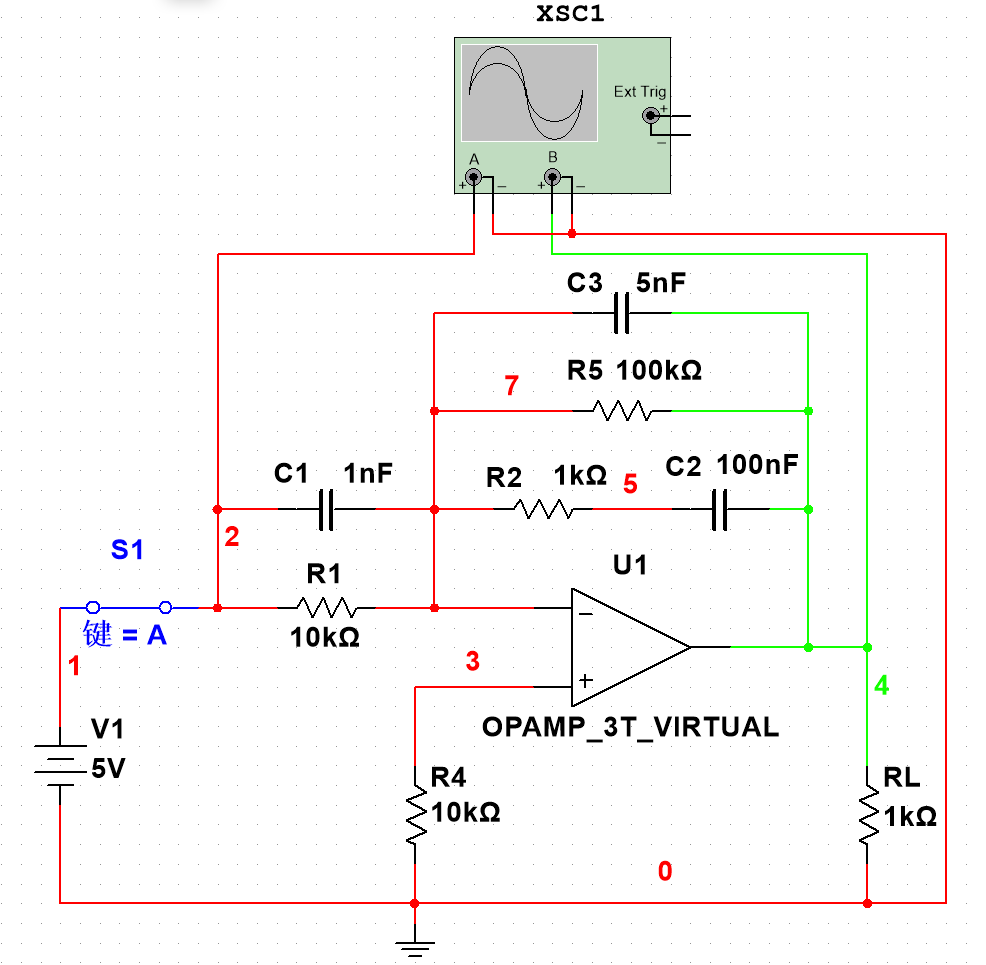
与前文的积分运算电路和微分运算电路相似，C3和R5在本电路中发挥着抑制低频（包括直流）和高频交流信号饱和的作用。

故在交流分析中，可忽略C3和R5两个原件所带来的影响。下面给出输出电压表达式：

if=iC1+iR1=C1du1dt+u1R1u4=−(uR2+uc2)=−(if∙R2+1C2∫ifdt)=−[(C1du1dt+u1R1)R2+1C2∫(C1du1dt+u1R1)dt]=−(R2R1+C1C2)u1−1C2∙R1∫u1dt−C1∙R2∙du1dt\begin{align*} i_f &=i_{C1}+i_{R1}=C_1\frac{du_1}{dt}+\frac{u_1}{R_1}\\\\ u_4 & =-\left(u_{R2}+u_{c2}\right)\\ & =-\left(i_f\bullet R_2+\frac{1}{C_2}\int{i_fdt}\right)\\ & =-[{(C}_1\frac{du_1}{dt}+\frac{u_1}{R_1})R_2+\frac{1}{C_2}\int{(C_1\frac{du_1}{dt}+\frac{u_1}{R_1})dt}]\\ & =-\left(\frac{R_2}{R_1}+\frac{C_1}{C_2}\right)u_1-\frac{1}{C_2\bullet R_1}\int{u_1dt{-C}_1\bullet}R_2\bullet\frac{du_1}{dt}\\ \end{align*}

比例系数 Kp=−(R2R1+C1C2)=−(1×10310×103+1×10−9100×10−9)=−0.11K_p=-\left(\frac{R_2}{R_1}+\frac{C_1}{C_2}\right)=-\left(\frac{1\times{10}^3}{10\times{10}^3}+\frac{1\times{10}^{-9}}{100\times{10}^{-9}}\right)=-0.11

积分系数 Ki=−1C2∙R1=−1100×10−9×10×103=−1000K_i=-\frac{1}{C_2\bullet R_1}=-\frac{1}{100\times{10}^{-9}\times10\times{10}^3}=-1000

微分系数 Kd=−C1∙R2=−1×10−9×1×103=−1×10−6K_d={-C}_1{\bullet R}_2=-1\times{10}^{-9}\times1\times{10}^3=-1{\times10}^{-6}

本文通过手动切换开关状态来达到模拟输入变化的情况，在开关A断开时，系统输入为零；当A闭合的瞬间，输入变化巨大，这就要求PID能够缓慢平稳地调整输出量，从而稳定输出波形。具体仿真结果如下图 9：

图 9 输入方波

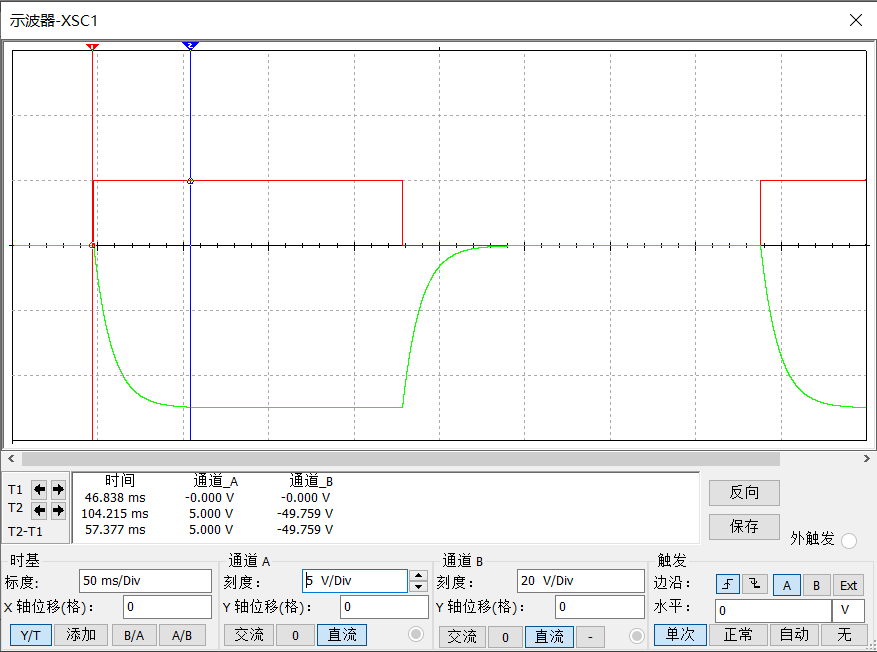
在46ms时，开关A突然闭合，可视为五个单位的阶跃信号，可见在面对输入信号如此大的变化时，良好的PID系统仍然能够稳定输出信号，平稳的控制输出量，经过60ms的响应时间便可使输出彻底稳定。对于输入突然减小的情况也同样发挥着极好的调节作用，充分说明调整良好的PID系统具有响应快、输出稳定的特点，同时也能避免超调、震荡等现象。

总结与展望

本文从PID控制原理开始引入，介绍了简单、运用广泛的两种PID控制算法，而后将重点置于利用所学完成PID控制电路的搭建和仿真，逐步实现PID控制电路，得到了不错的仿真效果，同时也极大地加深了对PID控制的了解。

近些年来，PID控制算法的设计得到了很大的发展，衍生出了一些改进型，例如专家型自适应PID算法、模糊PID算法等，都得到了很好的控制效果。[^6] [^7]但其应用有所丧失PID算法所保持的简便、清晰的特点，对使用者和系统都有格外的要求。例如模糊PID算法，需要格外设计相对应的模糊规则控制表， 相较于简单PID算法极大的提高了工作量，虽然控制效果得以有效提高，但对于简单运动控制，普通PID经过参数的整定也能取得不错的效果，模糊PID算法便丧失了其优势。

因此，未来PID的发展应向保持简便、易用的同时，努力提高控制效果的方向发展。而近年来深度学习和人工智能的长足发展，为PID控制算法的进一步发展指明了探索的方向，使其向着更加智能化的方向前进。

参考文献

[1] 兰野. 基于惯性轮式自行车的平衡与运动控制[D/OL]. 哈尔滨工业大学, 2021…

[2] 王伟, 张晶涛, 柴天佑. PID参数先进整定方法综述[J/OL]. 自动化学报, 2000(3): 347-355. DOI:10.16383/j.aas.2000.03.009.

[3] 杨智, 朱海锋, 黄以华. PID控制器设计与参数整定方法综述[J]. 化工自动化及仪表, 2005(5): 1-7.

[4] 王述彦, 师宇, 冯忠绪. 基于模糊PID控制器的控制方法研究[J/OL]. 机械科学与技术, 2011, 30(1): 166-172. DOI:10.13433/j.cnki.1003-8728.2011.01.035.

[5] 王祎晨. 增量式PID和位置式PID算法的整定比较与研究[J]. 工业控制计算机, 2018, 31(5): 123-124.

[6] 王蕾, 宋文忠. PID控制[J]. 自动化仪表, 2004(4): 3-8.

[7] 刘碧飞, 刘泓滨, 李华文. 基于模糊PID算法的智能车电机转速控制研究[J]. 农业装备与车辆工程, 2021, 59(1): 93-98.

[8] 白志刚. 自动调节系统解析与PID整定[M]. 化学工业出版社. 2012…